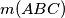
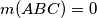
For three points in the plane, we define to be the smallest length of the three heights of the triangle , where in the case , , are collinear, we set . Let , , be given points in the plane. Prove that for any point in the plane,
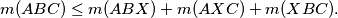
%V0
For three points $A,B,C$ in the plane, we define $m(ABC)$ to be the smallest length of the three heights of the triangle $ABC$, where in the case $A$, $B$, $C$ are collinear, we set $m(ABC) = 0$. Let $A$, $B$, $C$ be given points in the plane. Prove that for any point $X$ in the plane,
$$m(ABC) \leq m(ABX) + m(AXC) + m(XBC).$$
Source: Međunarodna matematička olimpijada, shortlist 1993
Školjka 
in the plane, we define 
to be the smallest length of the three heights of the triangle 
, where in the case 
, 
, 
are collinear, we set 
. Let 
in the plane, 