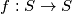
Let be the set of all real numbers strictly greater than −1. Find all functions satisfying the two conditions:
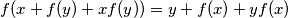
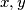
(a) for all in ;
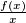
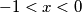
(b) is strictly increasing on each of the two intervals and .
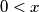
%V0
Let $S$ be the set of all real numbers strictly greater than −1. Find all functions $f: S \to S$ satisfying the two conditions:
(a) $f(x + f(y) + xf(y)) = y + f(x) + yf(x)$ for all $x, y$ in $S$;
(b) $\frac {f(x)}{x}$ is strictly increasing on each of the two intervals $- 1 < x < 0$ and $0 < x$.
Izvor: Međunarodna matematička olimpijada, shortlist 1994
Školjka 
be the set of all real numbers strictly greater than −1. Find all functions 
satisfying the two conditions: 
for all 
in 
is strictly increasing on each of the two intervals 
and 
.