Show that there exists a set of positive integers with the following property: for any infinite set of primes, there exist two positive integers in and not in , each of which is a product of distinct elements of for some .
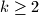
%V0
Show that there exists a set $A$ of positive integers with the following property: for any infinite set $S$ of primes, there exist two positive integers $m$ in $A$ and $n$ not in $A$, each of which is a product of $k$ distinct elements of $S$ for some $k \geq 2$.
Izvor: Međunarodna matematička olimpijada, shortlist 1994
Školjka 
of positive integers with the following property: for any infinite set 
of primes, there exist two positive integers 
in 
not in 
distinct elements of 
.