IMO Shortlist 1994 problem N5
Dodao/la:
arhiva2. travnja 2012. For any positive integer

, let
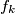
be the number of elements in the set
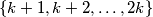
whose base 2 representation contains exactly three 1s.
(a) Prove that for any positive integer

, there exists at least one positive integer

such that
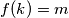
.
(b) Determine all positive integers

for which there exists exactly one

with
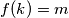
.
%V0
For any positive integer $k$, let $f_k$ be the number of elements in the set $\{ k + 1, k + 2, \ldots, 2k\}$ whose base 2 representation contains exactly three 1s.
(a) Prove that for any positive integer $m$, there exists at least one positive integer $k$ such that $f(k) = m$.
(b) Determine all positive integers $m$ for which there exists exactly one $k$ with $f(k) = m$.
Izvor: Međunarodna matematička olimpijada, shortlist 1994