IMO Shortlist 1995 problem A1
Dodao/la:
arhiva2. travnja 2012. Let

,

,

be positive real numbers such that
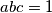
. Prove that
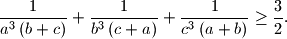
%V0
Let $a$, $b$, $c$ be positive real numbers such that $abc = 1$. Prove that $$\frac {1}{a^{3}\left(b + c\right)} + \frac {1}{b^{3}\left(c + a\right)} + \frac {1}{c^{3}\left(a + b\right)}\geq \frac {3}{2}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1995