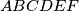
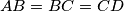
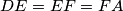
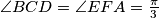
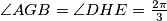
Let be a convex hexagon with and , such that . Suppose and are points in the interior of the hexagon such that . Prove that .
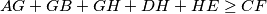
%V0
Let $ABCDEF$ be a convex hexagon with $AB = BC = CD$ and $DE = EF = FA$, such that $\angle BCD = \angle EFA = \frac {\pi}{3}$. Suppose $G$ and $H$ are points in the interior of the hexagon such that $\angle AGB = \angle DHE = \frac {2\pi}{3}$. Prove that $AG + GB + GH + DH + HE \geq CF$.
Izvor: Međunarodna matematička olimpijada, shortlist 1995
Školjka 
be a convex hexagon with 
and 
, such that 
. Suppose 
and 
are points in the interior of the hexagon such that 
. Prove that 
.