IMO Shortlist 1996 problem C1
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 We are given a positive integer  and a rectangular board
and a rectangular board  with dimensions
with dimensions 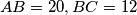 . The rectangle is divided into a grid of
. The rectangle is divided into a grid of 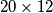 unit squares. The following moves are permitted on the board: one can move from one square to another only if the distance between the centers of the two squares is
unit squares. The following moves are permitted on the board: one can move from one square to another only if the distance between the centers of the two squares is 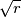 . The task is to find a sequence of moves leading from the square with
. The task is to find a sequence of moves leading from the square with  as a vertex to the square with
as a vertex to the square with  as a vertex.
as a vertex.
(a) Show that the task cannot be done if is divisible by 2 or 3.
is divisible by 2 or 3.
(b) Prove that the task is possible when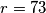 .
.
(c) Can the task be done when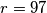 ?
?
 and a rectangular board
and a rectangular board  with dimensions
with dimensions 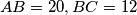 . The rectangle is divided into a grid of
. The rectangle is divided into a grid of 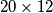 unit squares. The following moves are permitted on the board: one can move from one square to another only if the distance between the centers of the two squares is
unit squares. The following moves are permitted on the board: one can move from one square to another only if the distance between the centers of the two squares is 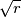 . The task is to find a sequence of moves leading from the square with
. The task is to find a sequence of moves leading from the square with  as a vertex to the square with
as a vertex to the square with  as a vertex.
as a vertex. (a) Show that the task cannot be done if
 is divisible by 2 or 3.
is divisible by 2 or 3. (b) Prove that the task is possible when
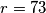 .
. (c) Can the task be done when
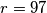 ?
? Izvor: Međunarodna matematička olimpijada, shortlist 1996
 Školjka
Školjka 
