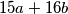
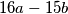
The positive integers and are such that the numbers and are both squares of positive integers. What is the least possible value that can be taken on by the smaller of these two squares?
%V0
The positive integers $a$ and $b$ are such that the numbers $15a + 16b$ and $16a - 15b$ are both squares of positive integers. What is the least possible value that can be taken on by the smaller of these two squares?
Izvor: Međunarodna matematička olimpijada, shortlist 1996
Školjka 
and 
are such that the numbers 
and 
are both squares of positive integers. What is the least possible value that can be taken on by the smaller of these two squares?