IMO Shortlist 1997 problem 4
Dodao/la:
arhiva2. travnja 2012. An

matrix whose entries come from the set
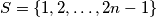
is called a silver matrix if, for each
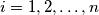
, the

-th row and the

-th column together contain all elements of

. Show that:
(a) there is no silver matrix for
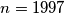
;
(b) silver matrices exist for infinitely many values of

.
%V0
An $n \times n$ matrix whose entries come from the set $S = \{1, 2, \ldots , 2n - 1\}$ is called a silver matrix if, for each $i = 1, 2, \ldots , n$, the $i$-th row and the $i$-th column together contain all elements of $S$. Show that:
(a) there is no silver matrix for $n = 1997$;
(b) silver matrices exist for infinitely many values of $n$.
Izvor: Međunarodna matematička olimpijada, shortlist 1997