IMO Shortlist 1997 problem 8
Kvaliteta:
Avg: 3,0Težina:
Avg: 6,0 It is known that 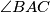 is the smallest angle in the triangle
is the smallest angle in the triangle  . The points
. The points  and
and  divide the circumcircle of the triangle into two arcs. Let
divide the circumcircle of the triangle into two arcs. Let  be an interior point of the arc between
be an interior point of the arc between  and
and  which does not contain
which does not contain  . The perpendicular bisectors of
. The perpendicular bisectors of  and
and  meet the line
meet the line 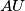 at
at  and
and  , respectively. The lines
, respectively. The lines 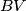 and
and 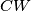 meet at
meet at  .
.
Show that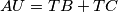 .
.
Alternative formulation:
Four different points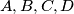 are chosen on a circle
are chosen on a circle  such that the triangle
such that the triangle  is not right-angled. Prove that:
is not right-angled. Prove that:
(a) The perpendicular bisectors of and
and  meet the line
meet the line  at certain points
at certain points  and
and 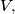 respectively, and that the lines
respectively, and that the lines 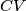 and
and 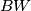 meet at a certain point
meet at a certain point 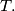
(b) The length of one of the line segments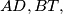 and
and 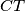 is the sum of the lengths of the other two.
is the sum of the lengths of the other two.
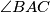 is the smallest angle in the triangle
is the smallest angle in the triangle  . The points
. The points  and
and  divide the circumcircle of the triangle into two arcs. Let
divide the circumcircle of the triangle into two arcs. Let  be an interior point of the arc between
be an interior point of the arc between  and
and  which does not contain
which does not contain  . The perpendicular bisectors of
. The perpendicular bisectors of  and
and  meet the line
meet the line 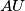 at
at  and
and  , respectively. The lines
, respectively. The lines 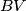 and
and 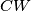 meet at
meet at  .
. Show that
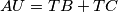 .
. Alternative formulation:
Four different points
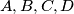 are chosen on a circle
are chosen on a circle  such that the triangle
such that the triangle  is not right-angled. Prove that:
is not right-angled. Prove that: (a) The perpendicular bisectors of
 and
and  meet the line
meet the line  at certain points
at certain points  and
and 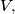 respectively, and that the lines
respectively, and that the lines 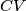 and
and 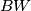 meet at a certain point
meet at a certain point 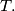
(b) The length of one of the line segments
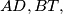 and
and 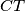 is the sum of the lengths of the other two.
is the sum of the lengths of the other two. Izvor: Međunarodna matematička olimpijada, shortlist 1997
 Školjka
Školjka 
