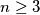
In a contest, there are candidates and judges, where is an odd integer. Each candidate is evaluated by each judge as either pass or fail. Suppose that each pair of judges agrees on at most candidates. Prove that
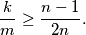
%V0
In a contest, there are $m$ candidates and $n$ judges, where $n\geq 3$ is an odd integer. Each candidate is evaluated by each judge as either pass or fail. Suppose that each pair of judges agrees on at most $k$ candidates. Prove that $${\frac{k}{m}} \geq {\frac{n-1}{2n}}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1998
Školjka 
candidates and 
judges, where 
is an odd integer. Each candidate is evaluated by each judge as either pass or fail. Suppose that each pair of judges agrees on at most 
candidates. Prove that 