IMO Shortlist 1998 problem G1
Dodao/la:
arhiva2. travnja 2012. A convex quadrilateral

has perpendicular diagonals. The perpendicular bisectors of the sides

and

meet at a unique point

inside

. Prove that the quadrilateral

is cyclic if and only if triangles
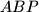
and
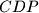
have equal areas.
%V0
A convex quadrilateral $ABCD$ has perpendicular diagonals. The perpendicular bisectors of the sides $AB$ and $CD$ meet at a unique point $P$ inside $ABCD$. Prove that the quadrilateral $ABCD$ is cyclic if and only if triangles $ABP$ and $CDP$ have equal areas.
Izvor: Međunarodna matematička olimpijada, shortlist 1998