IMO Shortlist 1999 problem N1
Dodao/la:
arhiva2. travnja 2012. Find all the pairs of positive integers
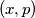
such that p is a prime,
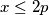
and
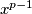
is a divisor of
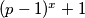
.
%V0
Find all the pairs of positive integers $(x,p)$ such that p is a prime, $x \leq 2p$ and $x^{p-1}$ is a divisor of $(p-1)^{x}+1$.
Izvor: Međunarodna matematička olimpijada, shortlist 1999