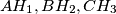
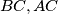
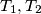
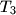
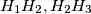
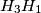
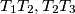
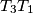
Let be the altitudes of an acute angled triangle . Its incircle touches the sides and at and respectively. Consider the symmetric images of the lines and with respect to the lines and . Prove that these images form a triangle whose vertices lie on the incircle of .
%V0
Let $AH_1, BH_2, CH_3$ be the altitudes of an acute angled triangle $ABC$. Its incircle touches the sides $BC, AC$ and $AB$ at $T_1, T_2$ and $T_3$ respectively. Consider the symmetric images of the lines $H_1H_2, H_2H_3$ and $H_3H_1$ with respect to the lines $T_1T_2, T_2T_3$ and $T_3T_1$. Prove that these images form a triangle whose vertices lie on the incircle of $ABC$.
Izvor: Međunarodna matematička olimpijada, shortlist 2000
Školjka 
be the altitudes of an acute angled triangle 
. Its incircle touches the sides 
and 
at 
and 
respectively. Consider the symmetric images of the lines 
and 
with respect to the lines 
and 
. Prove that these images form a triangle whose vertices lie on the incircle of