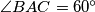
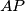
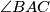
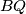
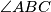
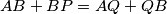
Let be a triangle with . Let bisect and let bisect , with on and on . If , what are the angles of the triangle?
%V0
Let $ABC$ be a triangle with $\angle BAC = 60^{\circ}$. Let $AP$ bisect $\angle BAC$ and let $BQ$ bisect $\angle ABC$, with $P$ on $BC$ and $Q$ on $AC$. If $AB + BP = AQ + QB$, what are the angles of the triangle?
Izvor: Međunarodna matematička olimpijada, shortlist 2001
Školjka 
be a triangle with 
. Let 
bisect 
and let 
bisect 
, with 
on 
and 
on 
. If 
, what are the angles of the triangle?