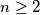
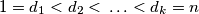
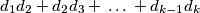
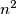
Let be a positive integer, with divisors . Prove that is always less than , and determine when it is a divisor of .
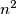
%V0
Let $n\geq2$ be a positive integer, with divisors $1=d_1<d_2<\,\ldots<d_k=n$. Prove that $d_1d_2+d_2d_3+\,\ldots\,+d_{k-1}d_k$ is always less than $n^2$, and determine when it is a divisor of $n^2$.
Izvor: Međunarodna matematička olimpijada, shortlist 2002
Školjka 
be a positive integer, with divisors 
. Prove that 
is always less than 
, and determine when it is a divisor of