IMO Shortlist 2003 problem A4
Dodao/la:
arhiva2. travnja 2012. Let

be a positive integer and let
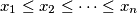
be real numbers.
Prove that
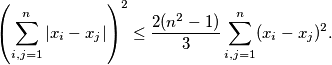
Show that the equality holds if and only if
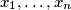
is an arithmetic sequence.
%V0
Let $n$ be a positive integer and let $x_1\le x_2\le\cdots\le x_n$ be real numbers.
Prove that
$$\left(\sum_{i,j=1}^{n}|x_i-x_j|\right)^2\le\frac{2(n^2-1)}{3}\sum_{i,j=1}^{n}(x_i-x_j)^2.$$
Show that the equality holds if and only if $x_1, \ldots, x_n$ is an arithmetic sequence.
Izvor: Međunarodna matematička olimpijada, shortlist 2003