IMO Shortlist 2005 problem C6
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,5 In a mathematical competition, in which 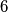 problems were posed to the participants, every two of these problems were solved by more than
problems were posed to the participants, every two of these problems were solved by more than  of the contestants. Moreover, no contestant solved all the
of the contestants. Moreover, no contestant solved all the 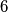 problems. Show that there are at least
problems. Show that there are at least  contestants who solved exactly
contestants who solved exactly 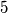 problems each.
problems each.
Radu Gologan and Dan Schwartz
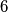 problems were posed to the participants, every two of these problems were solved by more than
problems were posed to the participants, every two of these problems were solved by more than  of the contestants. Moreover, no contestant solved all the
of the contestants. Moreover, no contestant solved all the 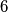 problems. Show that there are at least
problems. Show that there are at least  contestants who solved exactly
contestants who solved exactly 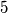 problems each.
problems each. Radu Gologan and Dan Schwartz
Izvor: Međunarodna matematička olimpijada, shortlist 2005
 Školjka
Školjka 
