IMO Shortlist 2005 problem N2
Dodao/la:
arhiva2. travnja 2012. Let
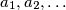
be a sequence of integers with infinitely many positive and negative terms. Suppose that for every positive integer

the numbers
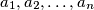
leave

different remainders upon division by

.
Prove that every integer occurs exactly once in the sequence
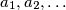
.
%V0
Let $a_1,a_2,\ldots$ be a sequence of integers with infinitely many positive and negative terms. Suppose that for every positive integer $n$ the numbers $a_1,a_2,\ldots,a_n$ leave $n$ different remainders upon division by $n$.
Prove that every integer occurs exactly once in the sequence $a_1,a_2,\ldots$.
Izvor: Međunarodna matematička olimpijada, shortlist 2005