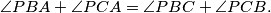
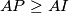
Let be triangle with incenter . A point in the interior of the triangle satisfies Show that , and that equality holds if and only if .
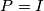
%V0
Let $ABC$ be triangle with incenter $I$. A point $P$ in the interior of the triangle satisfies $$\angle PBA+\angle PCA = \angle PBC+\angle PCB.$$ Show that $AP \geq AI$, and that equality holds if and only if $P=I$.
Izvor: Međunarodna matematička olimpijada, shortlist 2006
Školjka 
be triangle with incenter 
. A point 
in the interior of the triangle satisfies 
Show that 
, and that equality holds if and only if 
.