IMO Shortlist 2007 problem A1
Dodao/la:
arhiva2. travnja 2012. Real numbers
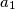
,
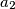
,

,
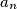
are given. For each

,
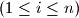
, define
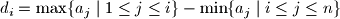
and let
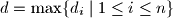
.
(a) Prove that, for any real numbers
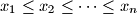
,
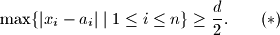
(b) Show that there are real numbers
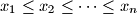
such that the equality holds in (*).
Author: Michael Albert, New Zealand
%V0
Real numbers $a_{1}$, $a_{2}$, $\ldots$, $a_{n}$ are given. For each $i$, $(1 \leq i \leq n )$, define
$$d_{i} = \max \{ a_{j}\mid 1 \leq j \leq i \} - \min \{ a_{j}\mid i \leq j \leq n \}$$
and let $d = \max \{d_{i}\mid 1 \leq i \leq n \}$.
(a) Prove that, for any real numbers $x_{1}\leq x_{2}\leq \cdots \leq x_{n}$,
$$\max \{ |x_{i} - a_{i}| \mid 1 \leq i \leq n \}\geq \frac {d}{2}. \quad \quad (*)$$
(b) Show that there are real numbers $x_{1}\leq x_{2}\leq \cdots \leq x_{n}$ such that the equality holds in (*).
Author: Michael Albert, New Zealand
Izvor: Međunarodna matematička olimpijada, shortlist 2007