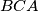
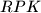
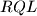
In triangle the bisector of angle intersects the circumcircle again at , the perpendicular bisector of at , and the perpendicular bisector of at . The midpoint of is and the midpoint of is . Prove that the triangles and have the same area.
Author: Marek Pechal, Czech Republic
%V0
In triangle $ABC$ the bisector of angle $BCA$ intersects the circumcircle again at $R$, the perpendicular bisector of $BC$ at $P$, and the perpendicular bisector of $AC$ at $Q$. The midpoint of $BC$ is $K$ and the midpoint of $AC$ is $L$. Prove that the triangles $RPK$ and $RQL$ have the same area.
Author: Marek Pechal, Czech Republic
Izvor: Međunarodna matematička olimpijada, shortlist 2007
Školjka 
the bisector of angle 
intersects the circumcircle again at 
, the perpendicular bisector of 
at 
, and the perpendicular bisector of 
at 
. The midpoint of 
and the midpoint of 
. Prove that the triangles 
and 
have the same area.