IMO Shortlist 2007 problem G4
Dodao/la:
arhiva2. travnja 2012. Consider five points

,

,

,

and

such that

is a parallelogram and
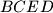
is a cyclic quadrilateral. Let
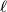
be a line passing through

. Suppose that
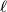
intersects the interior of the segment
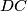
at

and intersects line

at

. Suppose also that
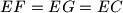
. Prove that
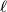
is the bisector of angle
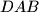
.
Author: Charles Leytem, Luxembourg
%V0
Consider five points $A$, $B$, $C$, $D$ and $E$ such that $ABCD$ is a parallelogram and $BCED$ is a cyclic quadrilateral. Let $\ell$ be a line passing through $A$. Suppose that $\ell$ intersects the interior of the segment $DC$ at $F$ and intersects line $BC$ at $G$. Suppose also that $EF = EG = EC$. Prove that $\ell$ is the bisector of angle $DAB$.
Author: Charles Leytem, Luxembourg
Izvor: Međunarodna matematička olimpijada, shortlist 2007