IMO Shortlist 2009 problem A3
Dodao/la:
arhiva2. travnja 2012. Determine all functions

from the set of positive integers to the set of positive integers such that, for all positive integers

and

, there exists a non-degenerate triangle with sides of lengths
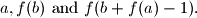
(A triangle is non-degenerate if its vertices are not collinear.)
Proposed by Bruno Le Floch, France
%V0
Determine all functions $f$ from the set of positive integers to the set of positive integers such that, for all positive integers $a$ and $b$, there exists a non-degenerate triangle with sides of lengths
$$a, f(b) \text{ and } f(b + f(a) - 1).$$
(A triangle is non-degenerate if its vertices are not collinear.)
Proposed by Bruno Le Floch, France
Izvor: Međunarodna matematička olimpijada, shortlist 2009