IMO Shortlist 2009 problem A6
Dodao/la:
arhiva2. travnja 2012. Suppose that
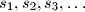
is a strictly increasing sequence of positive integers such that the sub-sequences
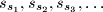
and
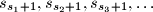
are both arithmetic progressions. Prove that the sequence
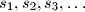
is itself an arithmetic progression.
Proposed by Gabriel Carroll, USA
%V0
Suppose that $s_1,s_2,s_3, \ldots$ is a strictly increasing sequence of positive integers such that the sub-sequences $s_{s_1},s_{s_2},s_{s_3},\ldots$ and $s_{s_1 + 1},s_{s_2 + 1},s_{s_3 + 1},\ldots$ are both arithmetic progressions. Prove that the sequence $s_1,s_2,s_3, \ldots$ is itself an arithmetic progression.
Proposed by Gabriel Carroll, USA
Izvor: Međunarodna matematička olimpijada, shortlist 2009