Let

be a positive integer and let

,

,
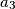
, ...,
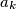
(
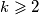
) be distinct integers in the set
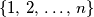
such that

divides
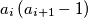
for
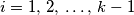
. Prove that

does not divide
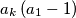
.
Proposed by Ross Atkins, Australia
%V0
Let $n$ be a positive integer and let $a_1$, $a_2$, $a_3$, ..., $a_k$ ($k \geqslant 2$) be distinct integers in the set $\left\{1,\,2,\,\ldots,\,n\right\}$ such that $n$ divides $a_i \left(a_{i + 1} - 1\right)$ for $i = 1,\,2,\,\ldots,\,k - 1$. Prove that $n$ does not divide $a_k \left(a_1 - 1\right)$.
Proposed by Ross Atkins, Australia