IMO Shortlist 2010 problem A7
Dodao/la:
arhiva23. lipnja 2013. Let
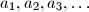
be a sequence of positive real numbers, and

be a positive integer, such that
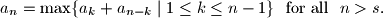
Prove there exist positive integers
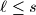
and

, such that
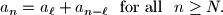
Proposed by Morteza Saghafiyan, Iran
%V0
Let $a_1, a_2, a_3, \ldots$ be a sequence of positive real numbers, and $s$ be a positive integer, such that
$$a_n = \max \{ a_k + a_{n-k} \mid 1 \leq k \leq n-1 \} \ \textrm{ for all } \ n > s.$$
Prove there exist positive integers $\ell \leq s$ and $N$, such that
$$a_n = a_{\ell} + a_{n - \ell} \ \textrm{ for all } \ n \geq N.$$
Proposed by Morteza Saghafiyan, Iran
Izvor: Međunarodna matematička olimpijada, shortlist 2010