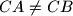
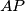
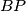
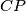
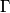
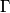
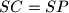
Let be a point interior to triangle (with ). The lines , and meet again its circumcircle at , , respectively . The tangent line at to meets the line at . Show that from follows .
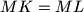
Proposed by Marcin E. Kuczma, Poland
%V0
Let $P$ be a point interior to triangle $ABC$ (with $CA \neq CB$). The lines $AP$, $BP$ and $CP$ meet again its circumcircle $\Gamma$ at $K$, $L$, respectively $M$. The tangent line at $C$ to $\Gamma$ meets the line $AB$ at $S$. Show that from $SC = SP$ follows $MK = ML$.
Proposed by Marcin E. Kuczma, Poland
Izvor: Međunarodna matematička olimpijada, shortlist 2010
Školjka 
be a point interior to triangle 
(with 
). The lines 
, 
and 
meet again its circumcircle 
at 
, 
, respectively 
. The tangent line at 
to 
at 
. Show that from 
follows 
.