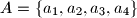
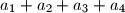
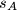
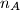
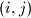
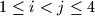
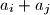
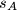
Given any set of four distinct positive integers, we denote the sum by . Let denote the number of pairs with for which divides . Find all sets of four distinct positive integers which achieve the largest possible value of .
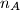
Proposed by Fernando Campos, Mexico
%V0
Given any set $A = \{a_1, a_2, a_3, a_4\}$ of four distinct positive integers, we denote the sum $a_1 +a_2 +a_3 +a_4$ by $s_A$. Let $n_A$ denote the number of pairs $(i, j)$ with $1 \leq i < j \leq 4$ for which $a_i +a_j$ divides $s_A$. Find all sets $A$ of four distinct positive integers which achieve the largest possible value of $n_A$.
Proposed by Fernando Campos, Mexico
Source: Međunarodna matematička olimpijada, shortlist 2011
Školjka 
of four distinct positive integers, we denote the sum 
by 
. Let 
denote the number of pairs 
with 
for which 
divides 
of four distinct positive integers which achieve the largest possible value of