IMO Shortlist 2011 problem C3
Kvaliteta:
Avg: 5,0Težina:
Avg: 4,0 Let 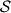 be a finite set of at least two points in the plane. Assume that no three points of
be a finite set of at least two points in the plane. Assume that no three points of 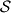 are collinear. A windmill is a process that starts with a line
are collinear. A windmill is a process that starts with a line 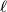 going through a single point
going through a single point 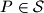 . The line rotates clockwise about the pivot
. The line rotates clockwise about the pivot  until the first time that the line meets some other point belonging to
until the first time that the line meets some other point belonging to 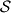 . This point,
. This point,  , takes over as the new pivot, and the line now rotates clockwise about
, takes over as the new pivot, and the line now rotates clockwise about  , until it next meets a point of
, until it next meets a point of 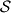 . This process continues indefinitely.
. This process continues indefinitely.
Show that we can choose a point in
in 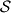 and a line
and a line 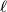 going through
going through  such that the resulting windmill uses each point of
such that the resulting windmill uses each point of 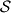 as a pivot infinitely many times.
as a pivot infinitely many times.
Proposed by Geoffrey Smith, United Kingdom
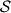 be a finite set of at least two points in the plane. Assume that no three points of
be a finite set of at least two points in the plane. Assume that no three points of 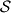 are collinear. A windmill is a process that starts with a line
are collinear. A windmill is a process that starts with a line 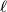 going through a single point
going through a single point 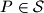 . The line rotates clockwise about the pivot
. The line rotates clockwise about the pivot  until the first time that the line meets some other point belonging to
until the first time that the line meets some other point belonging to 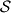 . This point,
. This point,  , takes over as the new pivot, and the line now rotates clockwise about
, takes over as the new pivot, and the line now rotates clockwise about  , until it next meets a point of
, until it next meets a point of 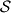 . This process continues indefinitely.
. This process continues indefinitely. Show that we can choose a point
 in
in 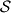 and a line
and a line 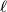 going through
going through  such that the resulting windmill uses each point of
such that the resulting windmill uses each point of 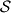 as a pivot infinitely many times.
as a pivot infinitely many times.Proposed by Geoffrey Smith, United Kingdom
Izvor: Međunarodna matematička olimpijada, shortlist 2011
 Školjka
Školjka 
