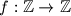
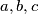
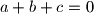
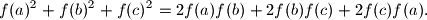
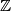
Find all functions such that, for all integers that satisfy , the following equality holds: (Here denotes the set of integers.)
Proposed by Liam Baker, South Africa
%V0
Find all functions $f:\mathbb Z\rightarrow \mathbb Z$ such that, for all integers $a,b,c$ that satisfy $a+b+c=0$, the following equality holds:
$$f(a)^2+f(b)^2+f(c)^2=2f(a)f(b)+2f(b)f(c)+2f(c)f(a).$$
(Here $\mathbb{Z}$ denotes the set of integers.)
Proposed by Liam Baker, South Africa
Source: Međunarodna matematička olimpijada, shortlist 2012
Školjka 
such that, for all integers 
that satisfy 
, the following equality holds:
denotes the set of integers.)