IMO Shortlist 2012 problem C6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 The liar's guessing game is a game played between two players  and
and  . The rules of the game depend on two positive integers
. The rules of the game depend on two positive integers  and
and  which are known to both players.
which are known to both players.
At the start of the game chooses integers
chooses integers  and
and  with
with 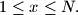 Player
Player  keeps
keeps  secret, and truthfully tells
secret, and truthfully tells  to player
to player  . Player
. Player  now tries to obtain information about
now tries to obtain information about  by asking player
by asking player  questions as follows: each question consists of
questions as follows: each question consists of  specifying an arbitrary set
specifying an arbitrary set  of positive integers (possibly one specified in some previous question), and asking
of positive integers (possibly one specified in some previous question), and asking  whether
whether  belongs to
belongs to  . Player
. Player  may ask as many questions as he wishes. After each question, player
may ask as many questions as he wishes. After each question, player  must immediately answer it with yes or no, but is allowed to lie as many times as she wants; the only restriction is that, among any
must immediately answer it with yes or no, but is allowed to lie as many times as she wants; the only restriction is that, among any 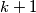 consecutive answers, at least one answer must be truthful.
consecutive answers, at least one answer must be truthful.
After has asked as many questions as he wants, he must specify a set
has asked as many questions as he wants, he must specify a set  of at most
of at most  positive integers. If
positive integers. If  belongs to
belongs to  , then
, then  wins; otherwise, he loses. Prove that:
wins; otherwise, he loses. Prove that:
1. If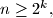 then
then  can guarantee a win.
can guarantee a win.
2. For all sufficiently large , there exists an integer
, there exists an integer 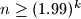 such that
such that  cannot guarantee a win.
cannot guarantee a win.
Proposed by David Arthur, Canada
 and
and  . The rules of the game depend on two positive integers
. The rules of the game depend on two positive integers  and
and  which are known to both players.
which are known to both players.At the start of the game
 chooses integers
chooses integers  and
and  with
with 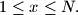 Player
Player  keeps
keeps  secret, and truthfully tells
secret, and truthfully tells  to player
to player  . Player
. Player  now tries to obtain information about
now tries to obtain information about  by asking player
by asking player  questions as follows: each question consists of
questions as follows: each question consists of  specifying an arbitrary set
specifying an arbitrary set  of positive integers (possibly one specified in some previous question), and asking
of positive integers (possibly one specified in some previous question), and asking  whether
whether  belongs to
belongs to  . Player
. Player  may ask as many questions as he wishes. After each question, player
may ask as many questions as he wishes. After each question, player  must immediately answer it with yes or no, but is allowed to lie as many times as she wants; the only restriction is that, among any
must immediately answer it with yes or no, but is allowed to lie as many times as she wants; the only restriction is that, among any 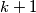 consecutive answers, at least one answer must be truthful.
consecutive answers, at least one answer must be truthful.After
 has asked as many questions as he wants, he must specify a set
has asked as many questions as he wants, he must specify a set  of at most
of at most  positive integers. If
positive integers. If  belongs to
belongs to  , then
, then  wins; otherwise, he loses. Prove that:
wins; otherwise, he loses. Prove that:1. If
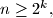 then
then  can guarantee a win.
can guarantee a win.2. For all sufficiently large
 , there exists an integer
, there exists an integer 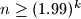 such that
such that  cannot guarantee a win.
cannot guarantee a win.Proposed by David Arthur, Canada
Izvor: Međunarodna matematička olimpijada, shortlist 2012
 Školjka
Školjka 
