Let
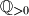
be the set of positive rational numbers. Let
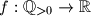
be a function satisfying the conditions
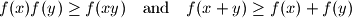
for all
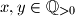
. Given that
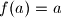
for some rational
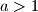
, prove that
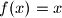
for all
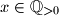
.
%V0
Let $\mathbb{Q}_{>0}$ be the set of positive rational numbers. Let $f : \mathbb{Q}_{>0} \to \mathbb{R}$ be a function satisfying the conditions $$
f(x) f(y) \geq f(xy) \quad \text{and} \quad f(x + y) \geq f(x) + f(y)
$$ for all $x, y \in \mathbb{Q}_{>0}$. Given that $f(a) = a$ for some rational $a > 1$, prove that $f(x) = x$ for all $x \in \mathbb{Q}_{>0}$.