IMO Shortlist 2013 problem G1
Kvaliteta:
Avg: 3,0Težina:
Avg: 6,0 Let  be an acute-angled triangle with orthocenter
be an acute-angled triangle with orthocenter  , and let
, and let  be a point on side
be a point on side  . Denote by
. Denote by  and
and  the feet of the altitudes from
the feet of the altitudes from  and
and  , respectively. Denote by
, respectively. Denote by 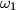 the circumcircle of
the circumcircle of 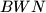 , and let
, and let  be the point on
be the point on 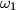 which is diametrically opposite to
which is diametrically opposite to  . Analogously, denote by
. Analogously, denote by 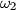 the circumcircle of
the circumcircle of 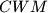 , and let
, and let  be the point on
be the point on 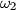 which is diametrically opposite to
which is diametrically opposite to  . Prove that
. Prove that  ,
,  and
and  are collinear.
are collinear.
 be an acute-angled triangle with orthocenter
be an acute-angled triangle with orthocenter  , and let
, and let  be a point on side
be a point on side  . Denote by
. Denote by  and
and  the feet of the altitudes from
the feet of the altitudes from  and
and  , respectively. Denote by
, respectively. Denote by 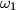 the circumcircle of
the circumcircle of 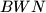 , and let
, and let  be the point on
be the point on 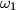 which is diametrically opposite to
which is diametrically opposite to  . Analogously, denote by
. Analogously, denote by 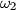 the circumcircle of
the circumcircle of 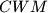 , and let
, and let  be the point on
be the point on 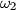 which is diametrically opposite to
which is diametrically opposite to  . Prove that
. Prove that  ,
,  and
and  are collinear.
are collinear. Izvor: Thailand
 Školjka
Školjka 
