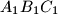
Let the excircle of the triangle lying opposite to touch its side at the point . Define the points and analogously. Suppose that the circumcentre of the triangle lies on the circumcircle of the triangle . Prove that the triangle is right-angled.
%V0
Let the excircle of the triangle $ABC$ lying opposite to $A$ touch its side $BC$ at the point $A_1$. Define the points $B_1$ and $C_1$ analogously. Suppose that the circumcentre of the triangle $A_1B_1C_1$ lies on the circumcircle of the triangle $ABC$. Prove that the triangle $ABC$ is right-angled.
Školjka 
lying opposite to 
touch its side 
at the point 
. Define the points 
and 
analogously. Suppose that the circumcentre of the triangle 
lies on the circumcircle of the triangle