IMO Shortlist 2010 problem G4
Given a triangle
, with
as its incenter and
as its circumcircle,
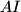
intersects
again at
. Let
be a point on the arc
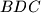
, and
a point on the segment
, such that
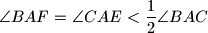
. If
is the midpoint of
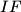
, prove that the meeting point of the lines
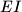
and
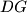
lies on
.
Proposed by Tai Wai Ming and Wang Chongli, Hong Kong
%V0
Given a triangle $ABC$, with $I$ as its incenter and $\Gamma$ as its circumcircle, $AI$ intersects $\Gamma$ again at $D$. Let $E$ be a point on the arc $BDC$, and $F$ a point on the segment $BC$, such that $\angle BAF=\angle CAE < \dfrac12\angle BAC$. If $G$ is the midpoint of $IF$, prove that the meeting point of the lines $EI$ and $DG$ lies on $\Gamma$.
Proposed by Tai Wai Ming and Wang Chongli, Hong Kong
Source: Međunarodna matematička olimpijada, shortlist 2010
Školjka 
