Neka su  i
i  duljine osnovica trapeza. Dokažite:
duljine osnovica trapeza. Dokažite:
a) Duljina dužine paralelne s osnovicama, koja raspolavlja površinu trapeza, jednaka je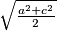 (kvadratna sredina).
(kvadratna sredina).
b) Duljina spojnice polovišta krakova jednaka je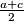 (aritmetička sredina).
(aritmetička sredina).
c) Duljina dužine paralelne osnovicama, koja dijeli trapez na dva međusobno slična trapeza, jednaka je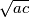 (geometrijska sredina).
(geometrijska sredina).
d) Duljina dužine paralelne s osnovicama kroz sjecište dijagonala, kojoj su krajevi na krakovima, jednaka je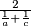 (harmonijska sredina).
(harmonijska sredina).
 i
i  duljine osnovica trapeza. Dokažite:
duljine osnovica trapeza. Dokažite:a) Duljina dužine paralelne s osnovicama, koja raspolavlja površinu trapeza, jednaka je
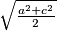 (kvadratna sredina).
(kvadratna sredina).b) Duljina spojnice polovišta krakova jednaka je
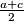 (aritmetička sredina).
(aritmetička sredina).c) Duljina dužine paralelne osnovicama, koja dijeli trapez na dva međusobno slična trapeza, jednaka je
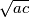 (geometrijska sredina).
(geometrijska sredina).d) Duljina dužine paralelne s osnovicama kroz sjecište dijagonala, kojoj su krajevi na krakovima, jednaka je
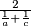 (harmonijska sredina).
(harmonijska sredina). Zadane su kružnica i tetiva koja dijeli njezinu nutrinu na dva kružna odsječka. U njih su upisane kružnice  i
i  koje iznutra diraju kružniuc
koje iznutra diraju kružniuc  , i danu tetivu diraju u istoj točki s raznih njezinih strana. Dokažite da je omjer polumjera kružnica
, i danu tetivu diraju u istoj točki s raznih njezinih strana. Dokažite da je omjer polumjera kružnica  i
i  konstantan, tj. da ne ovisi o položaju zajedničkog dirališta s tetivom.
konstantan, tj. da ne ovisi o položaju zajedničkog dirališta s tetivom.
 i
i  koje iznutra diraju kružniuc
koje iznutra diraju kružniuc  , i danu tetivu diraju u istoj točki s raznih njezinih strana. Dokažite da je omjer polumjera kružnica
, i danu tetivu diraju u istoj točki s raznih njezinih strana. Dokažite da je omjer polumjera kružnica  i
i  konstantan, tj. da ne ovisi o položaju zajedničkog dirališta s tetivom.
konstantan, tj. da ne ovisi o položaju zajedničkog dirališta s tetivom. Ivan i Krešo, pošli su istodobno iz Crikvenice u Kraljevicu, čija je udaljenost  km, a Marko je u isto vrijeme krenuo iz Kraljevice u Crikvenicu. Sva trojica imala su jedan bicikl i put su prevaljivali pješačenjem brzinom od
km, a Marko je u isto vrijeme krenuo iz Kraljevice u Crikvenicu. Sva trojica imala su jedan bicikl i put su prevaljivali pješačenjem brzinom od  km/h ili biciklom brzinom
km/h ili biciklom brzinom  km/h. Ivan je pošao pješice, dok je Krešo vozio bicikl sve dok se nije sreo s Markom. Tada je Krešo dao bicikl Marku i nastavio put prema Kraljevici pješice, a Marko je nastavio put prema Crikvenici biciklom. Kada je sreo Ivana dao mu je bicikl i ovaj je vozeći se stigao u Kraljevicu, dok je Marko pješice nastavio put do Crikvenice. Koliko vremena je svaki od njih trebao da dođe do svog cilja, koliko je pješačio, a koliko vozio bicikl?
km/h. Ivan je pošao pješice, dok je Krešo vozio bicikl sve dok se nije sreo s Markom. Tada je Krešo dao bicikl Marku i nastavio put prema Kraljevici pješice, a Marko je nastavio put prema Crikvenici biciklom. Kada je sreo Ivana dao mu je bicikl i ovaj je vozeći se stigao u Kraljevicu, dok je Marko pješice nastavio put do Crikvenice. Koliko vremena je svaki od njih trebao da dođe do svog cilja, koliko je pješačio, a koliko vozio bicikl?
 km, a Marko je u isto vrijeme krenuo iz Kraljevice u Crikvenicu. Sva trojica imala su jedan bicikl i put su prevaljivali pješačenjem brzinom od
km, a Marko je u isto vrijeme krenuo iz Kraljevice u Crikvenicu. Sva trojica imala su jedan bicikl i put su prevaljivali pješačenjem brzinom od  km/h ili biciklom brzinom
km/h ili biciklom brzinom  km/h. Ivan je pošao pješice, dok je Krešo vozio bicikl sve dok se nije sreo s Markom. Tada je Krešo dao bicikl Marku i nastavio put prema Kraljevici pješice, a Marko je nastavio put prema Crikvenici biciklom. Kada je sreo Ivana dao mu je bicikl i ovaj je vozeći se stigao u Kraljevicu, dok je Marko pješice nastavio put do Crikvenice. Koliko vremena je svaki od njih trebao da dođe do svog cilja, koliko je pješačio, a koliko vozio bicikl?
km/h. Ivan je pošao pješice, dok je Krešo vozio bicikl sve dok se nije sreo s Markom. Tada je Krešo dao bicikl Marku i nastavio put prema Kraljevici pješice, a Marko je nastavio put prema Crikvenici biciklom. Kada je sreo Ivana dao mu je bicikl i ovaj je vozeći se stigao u Kraljevicu, dok je Marko pješice nastavio put do Crikvenice. Koliko vremena je svaki od njih trebao da dođe do svog cilja, koliko je pješačio, a koliko vozio bicikl?  Školjka
Školjka 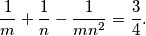
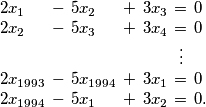
 i
i  vrijedi nejednakost
vrijedi nejednakost 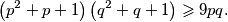
 s duljinom hipotenuze
s duljinom hipotenuze  upisan je kvadrat
upisan je kvadrat 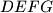 sa dva susjedna vrha
sa dva susjedna vrha  ,
,  na hipotenuzi
na hipotenuzi  i po jednim vrhom
i po jednim vrhom  i
i  na katetama
na katetama  i
i  . Izračunajte duljinu
. Izračunajte duljinu  stranice tog kvadrata i dokažite jednakost
stranice tog kvadrata i dokažite jednakost 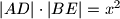 .
. 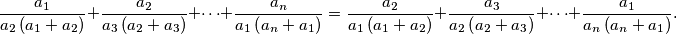
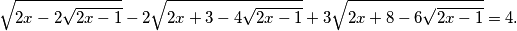
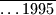 djeljiv sa
djeljiv sa 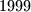 .
. 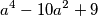 djeljiv s
djeljiv s 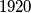 za svaki prosti broj
za svaki prosti broj 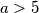 .
.  ,
,  zadovoljavaju relaciju
zadovoljavaju relaciju 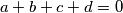 . Neka je
. Neka je 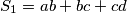 i
i 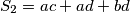 . Pokažite da je
. Pokažite da je 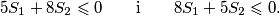
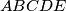 . Neka su
. Neka su  ,
,  ,
,  ,
,  redom polovišta stranica
redom polovišta stranica  ,
, 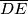 te neka su
te neka su  i
i  polovišta dužina
polovišta dužina 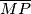 i
i 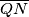 . Pokažite da je
. Pokažite da je 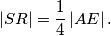
 kruga polumjera
kruga polumjera  jednakostraničnog trokuta duljine stranice
jednakostraničnog trokuta duljine stranice  prirodan broj. Nađite sva rješenja jednandžbe
prirodan broj. Nađite sva rješenja jednandžbe 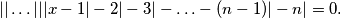
 . Odredite sve mogućnosti izbora brojeva
. Odredite sve mogućnosti izbora brojeva  ,
,  za koje je
za koje je 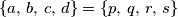 , a vrijednost izraza
, a vrijednost izraza 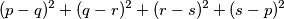 je najmanja.
je najmanja. 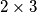 pravokutniku točno dva kvadratića su crvena. Promatrajte bilo koji
pravokutniku točno dva kvadratića su crvena. Promatrajte bilo koji 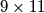 pravokutnik. Koliko u njemu ima crvenih kvadratića?
pravokutnik. Koliko u njemu ima crvenih kvadratića? 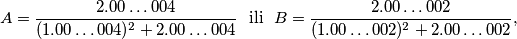 gdje u svakom broju u brojniku i nazivniku ima po
gdje u svakom broju u brojniku i nazivniku ima po 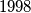 nula?
nula?  i
i 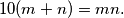
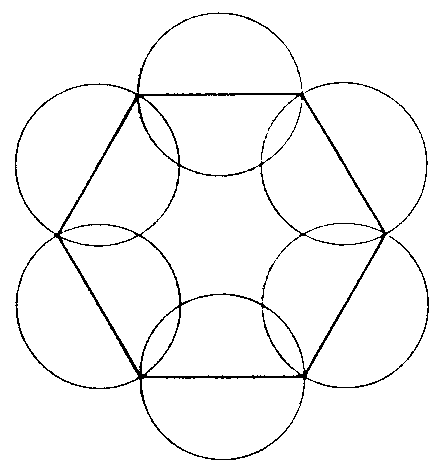
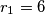 i
i 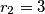 dodiruju se izvana. obje kruznice dodiruju iznutra kruznicu
dodiruju se izvana. obje kruznice dodiruju iznutra kruznicu 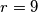 . zajednica vanjska tangenta kruznica
. zajednica vanjska tangenta kruznica 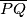 .
. 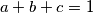 . Dokažite da vrijedi nejednakost
. Dokažite da vrijedi nejednakost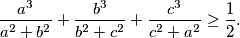
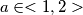 povrsina lika kojeg omeduju grafovi funkcija
povrsina lika kojeg omeduju grafovi funkcija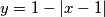 , te
, te 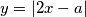

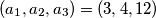 . Provodimo sljedeći postupak: biramo dva broja,
. Provodimo sljedeći postupak: biramo dva broja,  i
i 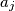 ,
, 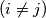 , te ih zamijenimo sa
, te ih zamijenimo sa 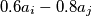 i
i 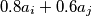 . Može li se višekratnom primjenom gore opisanog postupka dobiti trojka
. Može li se višekratnom primjenom gore opisanog postupka dobiti trojka 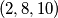 ?
? 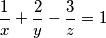 u skupu prirodnih brojeva.
u skupu prirodnih brojeva.  ,
,  i
i  . Izrazite kutove trokuta
. Izrazite kutove trokuta 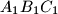 pomoću kutova trokuta
pomoću kutova trokuta 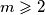 prirodan broj. Koliko rješenja u skupu prirodnih brojeva ima jednadžba
prirodan broj. Koliko rješenja u skupu prirodnih brojeva ima jednadžba 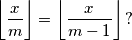
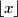 je oznaka za najveći cijeli broj koji nije veći od
je oznaka za najveći cijeli broj koji nije veći od  ,
,  ,
,  ,
,  ,
,  lipa i od
lipa i od 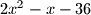 kvadrat prostog broja?
kvadrat prostog broja?  je točka
je točka  i
i 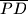 , a
, a  i
i 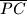 . Četverokutu
. Četverokutu 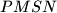 upisana je kružnica. Dokažite da je njen polumjer jednak
upisana je kružnica. Dokažite da je njen polumjer jednak 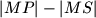 .
.