Simulacija HMO 2019
Neka je  konveksan četverokut takav da
konveksan četverokut takav da  nije paralelno s
nije paralelno s  . Neka je
. Neka je  presjek njegovih dijagonala, a
presjek njegovih dijagonala, a  presjek pravaca
presjek pravaca  i
i  . Pretpostavimo da u unutrašnjosti
. Pretpostavimo da u unutrašnjosti  postoji točka
postoji točka  takva da njezine projekcije na stranice
takva da njezine projekcije na stranice  čine pravokutnik. Neka je opisana kružnica tog pravokutnika
čine pravokutnik. Neka je opisana kružnica tog pravokutnika  .
.  i
i  su sjecišta
su sjecišta  s
s  i
i  , redom.
, redom.  je presjek tangenta na
je presjek tangenta na  u
u  i
i  . Dokažite da
. Dokažite da  leži na pravcu
leži na pravcu  .
.
Na ploči je zapisano  uzatopnih prirodnih brojeva. Dozvoljen potez je odbrati dva broja napisana na pločim, nazovimo ih
uzatopnih prirodnih brojeva. Dozvoljen potez je odbrati dva broja napisana na pločim, nazovimo ih  i
i  , i zamijeniti ih s brojevima
, i zamijeniti ih s brojevima 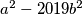 i
i 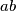 . Nakon nekog broja poteza, na ploči nema niti jednog broja koji je inicijalno bio zapisan na njoj. Je li moguće da se u tom trenutku na ploči ponovno nalazi
. Nakon nekog broja poteza, na ploči nema niti jednog broja koji je inicijalno bio zapisan na njoj. Je li moguće da se u tom trenutku na ploči ponovno nalazi  uzastopnih prirodnih brojeva?
uzastopnih prirodnih brojeva?
Neka su  i
i  središte upisane kružnice i ortocentar trokuta
središte upisane kružnice i ortocentar trokuta  , redom. Neka su
, redom. Neka su  i
i  polovišta stranica
polovišta stranica  i
i  , redom. Pravci
, redom. Pravci 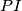 i
i 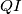 sijeku pravce
sijeku pravce  i
i  u točkama
u točkama  i
i  , redom. Neka je
, redom. Neka je  središte opisane kružnice trokuta
središte opisane kružnice trokuta 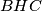 . Pravac
. Pravac 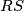 siječe dužinu
siječe dužinu  u točki
u točki  . Dokažite:
. Dokažite: 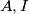 i
i  su kolinearne ako i samo ako trokuti
su kolinearne ako i samo ako trokuti 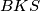 i
i 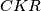 imaju jednake površine.
imaju jednake površine.
U grupi od  učenika, neki su prijatelji (prijateljstvo je uzajamno). Neku su
učenika, neki su prijatelji (prijateljstvo je uzajamno). Neku su 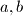 minimalni prirodni brojevi koji zadovoljavaju sljedeće uvjete:
minimalni prirodni brojevi koji zadovoljavaju sljedeće uvjete:
(1) Možemo podijeliti učenike u  timova tako da su unutar svake grupe svi bilo koja dva učenika prijatelji.
timova tako da su unutar svake grupe svi bilo koja dva učenika prijatelji.
(2) Možemo podijeliti učenike u  timova tako da su unutar svake grupe svi bilo koja dva učenika nisu prijatelji.
timova tako da su unutar svake grupe svi bilo koja dva učenika nisu prijatelji.
Odredite maksimalnu moguću vrijednost 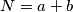 , u ovisnosti o
, u ovisnosti o  .
.
Neka je  središte opisane kružnice šiljastokutnog trokuta
središte opisane kružnice šiljastokutnog trokuta  , u kojem vrijedi
, u kojem vrijedi  . Simetrala kuta
. Simetrala kuta  sječe stranicu
sječe stranicu  u točki
u točki  .
.  je polovište dužine
je polovište dužine 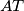 .
.  je točka u unutrašnjosti trokuta
je točka u unutrašnjosti trokuta  takva da je
takva da je 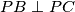 .
. 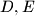 su točke koje leže na okomici iz
su točke koje leže na okomici iz  na
na 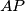 takve da vrijedi
takve da vrijedi 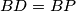 i
i 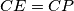 . Ako
. Ako 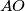 raspolavlja dužinu
raspolavlja dužinu  , dokažite da je
, dokažite da je 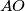 tangenta na opisanu kružnicu trokuta
tangenta na opisanu kružnicu trokuta 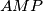 .
.
 Školjka
Školjka 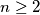 prirodan broj. Odredite sve funkcije
prirodan broj. Odredite sve funkcije 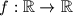 takve da za sve
takve da za sve 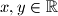 vrijedi
vrijedi 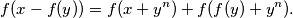
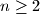 prirodan broj. Na kružnici se nalazi
prirodan broj. Na kružnici se nalazi 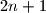 točaka koje ju dijele na lukove jednake duljine.
točaka koje ju dijele na lukove jednake duljine. 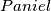 i
i 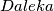 naizmjenice brišu točke s kružnice, s tim da
naizmjenice brišu točke s kružnice, s tim da 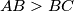 . Neka je
. Neka je  opisana kružnica trokuta
opisana kružnica trokuta  i
i  se sijeku u
se sijeku u 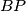 i
i 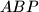 , a
, a  opisana kružnica trokuta
opisana kružnica trokuta 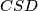 . Pretpostavite da se
. Pretpostavite da se 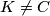 . Dokažite:
. Dokažite: 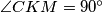 .
. 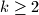 , odredite najveći mogući broj djelitelja kojeg broj
, odredite najveći mogući broj djelitelja kojeg broj 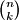 može imati u skupu
može imati u skupu 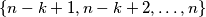 , gdje je
, gdje je 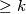 .
. 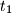 i
i 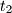 u
u 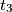 u
u 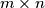 pravokutnoj ploči, gdje su
pravokutnoj ploči, gdje su  i
i 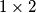 i
i 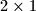 domina tako da prekrivaju sva osim jednog kutnog polja ploče. Dozvoljeni potezi su:
domina tako da prekrivaju sva osim jednog kutnog polja ploče. Dozvoljeni potezi su:  Dokažite da je moguće nizom takvih poteza postići da je bilo koje kutno polje ploče prazno.
Dokažite da je moguće nizom takvih poteza postići da je bilo koje kutno polje ploče prazno. 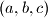 takve da vrijedi
takve da vrijedi 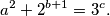
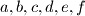 positivni realni brojevi. Ako je
positivni realni brojevi. Ako je 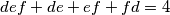 , dokažite da vrijedi
, dokažite da vrijedi 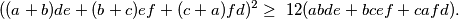
 prost broj,
prost broj, 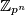 skup ostataka modulo
skup ostataka modulo 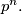 Odredite broj funkcija
Odredite broj funkcija 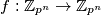 za koje vrijedi
za koje vrijedi 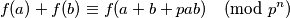 za sve
za sve 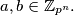
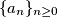 takav da je
takav da je 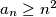 za svaki
za svaki 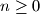 . Za sve
. Za sve 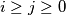 postoje
postoje 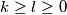 takvi da vrijedi:
takvi da vrijedi: 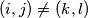
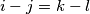
 .
. 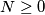 takav da vrijedi
takav da vrijedi 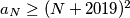 .
. 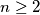 prirodnih brojeva
prirodnih brojeva 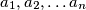 takvih da vrijedi
takvih da vrijedi 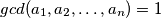 . Dozvoljena operacija je dodati nekom broju najveći zajednički djelitelj njegovih susjeda. Dokažite da je moguće u konačno mnogo operacija postići da su svi brojevi na kružnici u parovima relativno prosti.
. Dozvoljena operacija je dodati nekom broju najveći zajednički djelitelj njegovih susjeda. Dokažite da je moguće u konačno mnogo operacija postići da su svi brojevi na kružnici u parovima relativno prosti.